Продолжаю изучать влияние нелинейных искажений на гармонические колебания. Благодаря помощи здесь на форуме я узнал что при прохождении через нелинейный элемент гармонического сигнала его спектр обогащается гармониками. Также я узнал что при прохождении бигармонического сигнала через нелинейный элемент в спектре формируются комбинационные частоты (w2-w1) и (w2+w1) и их гармоники в дополнение к гармоникам исходных сигналов.
Теперь в первую очередь я хотел изучить влияние на спектр (пока только гармонического сигнала) нелинейного искажения, а именно отсечения. Для этого я написал небольшую программу в которой я и производил генерацию и модификацию сигнала, но столкнулся с проблемой. Исходя из описания здесь видно что амплитуда гармоник изменяется согласно функциям Берга при обрезании гармонического сигнала, там же есть графики первых 5 гармоник:
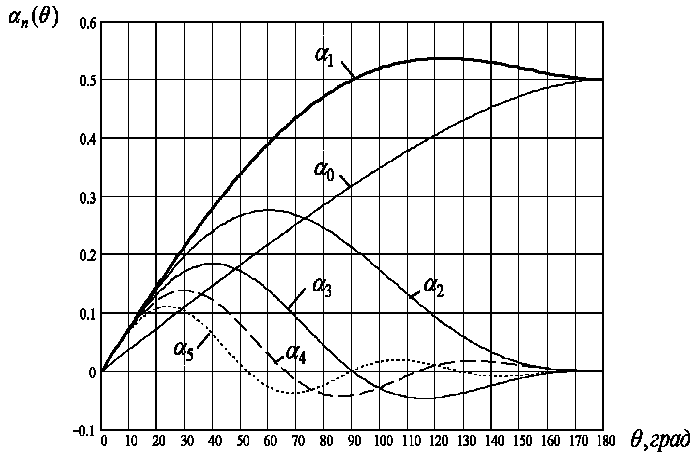
В своей программе я также сгенерировал гармоническое колебание, в цикле произвел его обрезку линейно изменяя угол отсечки, и произвел измерение спектра (используя FFT) гармоник сигнала, но у меня получился похожий, но немного другой график. У меня волны на графике симметричны, а волны в графике в статье затухают при увеличении угла отсечки.
Заполнение массива сигнала с отсечением согласно углу отсечки: Гармоники считаю так: Вот что выходит у меня: Где я мог ошибиться или это в статье график неправильный?
Заранее спасибо!
