Здравствуйте! Я понимаю что тема наверное многократно затрагивалась, более того я на форуме нашел похожую тему,
viewtopic.php?t=7130 но все же есть один вопрос. Мне понятны доказательства бесконечности спектра ограниченного по времени сигнала, приведенные в топике выше, но в одной книге, а именно Теория сигналов. Л. Френкс. 1974. нашел такой довод.
Инженерам по электросвязи хорошо известно что невозможно получить сигнал, ограниченный и по времени и по частоте.
И, далее приводится следующий интеграл:
= \int_{-T}^{T}x\left ( t \right )\cdot e^{-i\cdot 2\cdot \pi \cdot f\cdot t}\cdot dt)
При этом утверждается что данный интеграл может быть равен нулю лишь при некоторых значениях частоты
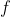
. И вот я никак не могу до конца осмыслить как правильно проанализировать этот интеграл. По моему мнению если например сигнал является на ограниченном интервале функцией общего вида (не четный и не нечетный) то интеграл в принципе не может быть равен нулю ни при каком значении
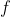
. То есть видимо только при четном или нечетном сигнале
)
возможен нуль на определенной частоте
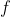
. Но вот никак не могу точно проанализировать функцию
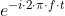
. Получается что она всегда общего вида ?? Или я неправ. Даже если по формуле Эйлера представить экспоненту непонятно как в получающейся разности двух интегралов получить нуль. Сразу оговорюсь вариант когда исходный сигнал тождественный нуль не рассматривается. Буду рад любой информации.
