Доброго времени суток. ОПФ от функции F(-w), будет -1/(2*pi)* x(-t) ???
где x(-t) - сопряжённое.
Интеграл по отрицательному аргументу
Интеграл по отрицательному аргументу
Последний раз редактировалось abraziv 19 авг 2017, 03:02, всего редактировалось 1 раз.
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Интеграл по отрицательному аргументу
Нет если $x^*(t)$ комплексно сопряженый сигнал то его спектр равен $X^*(-w) $ Т.е не просто инвертирование по частоте но и сопряжен
Re: Интеграл по отрицательному аргументу
Это я понимаю. Интересует, что будет с сигналом во временной области если его спектр F(w) будет инвертирован, т.е. F(-w).
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Интеграл по отрицательному аргументу
Думается что -x(-t). В выкладках не уверен если надо вечером напишу выкладки
Re: Интеграл по отрицательному аргументу
Хм. Да надо, если не жалко. Но вот почему ответ в моём первом посте Вам не понравился. Если поменять знак у экспоненты в интеграле Фурье, то получим же сопряжённый? Если да, то я правильно посчитал:
* x(-t)^* )
Просто -t в вашем выражении меня очень смущает, думаю, как это физически интерпретировать. Если спектр сигнала инвертирован, то он во временной области тоже инвертируется во времени (!!!!!!!!!!!???) и инвертирует амплитуду??? Что-то не то.
Завтра матлаб запущу, посчитаю численно, там покажет, кто прав=)))
Просто -t в вашем выражении меня очень смущает, думаю, как это физически интерпретировать. Если спектр сигнала инвертирован, то он во временной области тоже инвертируется во времени (!!!!!!!!!!!???) и инвертирует амплитуду??? Что-то не то.
Завтра матлаб запущу, посчитаю численно, там покажет, кто прав=)))
Последний раз редактировалось abraziv 19 авг 2017, 03:01, всего редактировалось 1 раз.
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Интеграл по отрицательному аргументу
мои выкладки:
Пусть сигнал) представляется через обратное преобразование Фурье своего спектра
представляется через обратное преобразование Фурье своего спектра ) :
:
 = \frac{1}{2\pi}\int_{-\infty}^{\infty} X(w) \cdot \exp( jwt) dw)
Тогда рассмотрим что будет с сигналом если спектр) :
:
 \cdot \exp( jwt) dw)
Сделаем замену переменной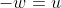 , тогда
, тогда 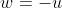 и
и 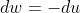 . Подставим и получим
. Подставим и получим
 \cdot \exp( -jut) du)
Сделаем еще одну замену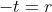 и тогда получим
и тогда получим
 \cdot \exp( jur) du = -x(r) = -x(-t) )
Пусть сигнал
Тогда рассмотрим что будет с сигналом если спектр
Сделаем замену переменной
Сделаем еще одну замену
Re: Интеграл по отрицательному аргументу
Спасибо. Как можно физически интерпретировать результат?
Re: Интеграл по отрицательному аргументу
Сергей, ну так всё таки. Пусть есть комплексный спектр ) расположенный в основной полосе частот, т.е. он не симметричен относительно начала координат и оси ординат. Этому спектру соответствует сигнал во временном домене
расположенный в основной полосе частот, т.е. он не симметричен относительно начала координат и оси ординат. Этому спектру соответствует сигнал во временном домене ) . Теперь берём этот спектр и инвертируем, что случится с
. Теперь берём этот спектр и инвертируем, что случится с ) =)))) Математически
=)))) Математически ) , а вот физически не понятно =))))
, а вот физически не понятно =))))
Это же эквивалентно, отличию LSB от USB, в основной полосе частот.
Это же эквивалентно, отличию LSB от USB, в основной полосе частот.
Re: Интеграл по отрицательному аргументу
Можно интерпретировать, как  = cos(t) + j sin(t)) , тогда
, тогда ) =
=  + j sin (-t))) =
=  - j sin(t))) =
= +j sin(t))
Тогда смысл, таков, что инвертирование спектра есть сопряжение и инвертирование амплитуды во временной области!!!
Нужно только понимать, что для полосового сигнала:
 = F(-w))
Для комплексного базбенда:
 = F^*(-w))
Тогда смысл, таков, что инвертирование спектра есть сопряжение и инвертирование амплитуды во временной области!!!
Нужно только понимать, что для полосового сигнала:
Для комплексного базбенда:
