Амплитуда гармонического сигнала.
Амплитуда гармонического сигнала.
Скажите пожалуйста, амплитуда к-й гармоники сигнала равна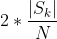 или
или 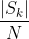 ? Вроде как
? Вроде как +Arg(e))) , однако вот тут без двойки. И здесь , правда косвенно, тоже без двойки.
, однако вот тут без двойки. И здесь , правда косвенно, тоже без двойки.
Дмитрий Беловол
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Амплитуда гармонического сигнала.
не совсем понял что такое  и
и 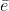 в ваших рассуждениях, но правильно амплитуду нормировать как
в ваших рассуждениях, но правильно амплитуду нормировать как 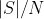
Re: Амплитуда гармонического сигнала.
здесь дана формула ОБПФ
для
Учитывая, что
и принимая во внимание тождество из предыдущего поста, получаем (Пусть N-нечетное):
Где ошибся?
Дмитрий Беловол
Re: Амплитуда гармонического сигнала.
S(i) и S(N-i) это две разных частоты.
Re: Амплитуда гармонического сигнала.
Это два разных комплексных спектральных отсчета, которые соответствуют одной и той же частоте в исходном сигнале. Точнее, если у вас частота синусоидального сигнала F меньше половины частоты дискретизации F1 и время забора кратно периоду синусоидального сигнала, то в результате ДПФ вы получите два комплексных отсчета, равных по модулю. Один будет иметь номер F*T, а другой (F1-F)*T. Но ведь из этого не следует, что в исходном сигнале у вас было две частоты. Другими словами, сигналы на частоте F и на частоте F1-F после дискретизации на частоте F1 будут неотличимы.
Мой вопрос относится к модулю этих двух отсчетов. Я не понимаю, почему он равен амплитуде исходного сигнала. Из формул ДПФ следует, что он должен быть равен половине этой амплитуды (вроде бы следует ), умноженной на N
), умноженной на N
Мой вопрос относится к модулю этих двух отсчетов. Я не понимаю, почему он равен амплитуде исходного сигнала. Из формул ДПФ следует, что он должен быть равен половине этой амплитуды (вроде бы следует
Дмитрий Беловол
Re: Амплитуда гармонического сигнала.
Еще раз повторяю это две разные частоты F и -F. И то что их модуль совпадает это особенность действительного сигнала IM=0. Однако подайте на вход комплексный сигнал и модули не совпадут.
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Амплитуда гармонического сигнала.
спектральные отсчеты с номерами от N/2 до N-1 соответствуют отрицательным частотам в спектре. Для вещественного сигнала амплитудный спектр всегда симметричен относительно нуля поскольку cos(w*t) = cos(-w*t). В результате для сигнала s(t) = cos(w*t) в спектре появляется 2 палки одна на частоте w а вторая на частоте -w. амплитуда каждой палки будет равна 0.5. В случае ДПФ вы видите 2 палки одна на спектральном отсчете k а вторая на спектральном отсчете N-k-1. Каждая из палок будет половинной амплитуды. Но если вы возьмете комплексный сигнал например s(t) = exp(j*w*t) = cos(w*t)+j*sin(w*t) то получим только одну палку на частоте w полной амплитуды равной 1.dbelovol писал(а):Это два разных комплексных спектральных отсчета, которые соответствуют одной и той же частоте в исходном сигнале. Точнее, если у вас частота синусоидального сигнала F меньше половины частоты дискретизации F1 и время забора кратно периоду синусоидального сигнала, то в результате ДПФ вы получите два комплексных отсчета, равных по модулю. Один будет иметь номер F*T, а другой (F1-F)*T. Но ведь из этого не следует, что в исходном сигнале у вас было две частоты. Другими словами, сигналы на частоте F и на частоте F1-F после дискретизации на частоте F1 будут неотличимы.
Мой вопрос относится к модулю этих двух отсчетов. Я не понимаю, почему он равен амплитуде исходного сигнала. Из формул ДПФ следует, что он должен быть равен половине этой амплитуды (вроде бы следует), умноженной на N
Re: Амплитуда гармонического сигнала.
Я имею дело с вещественными сигналами, так что двойка нужна. Хорошо. А вот еще вопрос. В этой статье в описании первого графика на рис.3. сказано, что"...При дискретизации получим только отсчет...... по амплитуде соответствующий амплитуде сигнала...". Почему не сказано "два отсчета, по амплитуде равных половине амплитуды сигнала"? Там же тоже речь о вещественном сигнале.
Дмитрий Беловол
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Амплитуда гармонического сигнала.
1. Двойка НЕ нужна. В противном случае вы нарушаете равенство Парсеваля и мощность вашего сигнала в частотной области будет в 2 раза выше мощности во временной.dbelovol писал(а):Я имею дело с вещественными сигналами, так что двойка нужна. Хорошо. А вот еще вопрос. В этой статье в описании первого графика на рис.3. сказано, что"...При дискретизации получим только отсчет...... по амплитуде соответствующий амплитуде сигнала...". Почему не сказано "два отсчета, по амплитуде равных половине амплитуды сигнала"? Там же тоже речь о вещественном сигнале.
2. В приведенной статье рассматривается совсем другой вопрос и другой эффект, поэтому фраза "один отсчет" означает что в спектре не наблюдается растекания (палка не размазана по частоте). Что касается амплитуды то слово "соответствующий" и слово "равный" это два разных слова. Я думаю вы в состоянии оценить разницу.
3. Я предлагаю перейти в русло конструктивнго обсуждения а не придираться, выдергивать фразы из контекста.
