ИХ фильтра Гаусса
Re: ИХ фильтра Гаусса
ок. договорились. выложу как только закончу с демом. щас есть некоторые трудности, т.к. в наличии есть только одна реализация GSM сигнала, да и тот по всей видимости сгенерирован искусственно, реальными сигналами пока не обладаю. а как известно, GSM это TDMA сигнал, а значит работает в пакетном режиме, что еще немного усложняет демодулятор. а самому писать модулятор для непрерывного режима что-то не очень хочется, хотя может и придется все-таки. в любом случае результатами поделюсь.
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: ИХ фильтра Гаусса
Ну что-же в данном длинном посте я постараюсь изложить свои соображения по поводу ких фильтра Гаусса для GMSK.
Поскольку в разных источниках этот фильтр описан немного по-разному необходимо дать пояснения. Я буду опираться на матлаб и на собственную реализацию фильтра Гаусса, которые немного отличаются, я поясню в дальнейшем в чем именно. В матлабе фильтр Гаусса задается функцией gaussfir, в хелпе на нее написано следующее:
итак есть 3 параметра:
BT - ширина полосы фильтра по уровню -3 дБ умноженная на длительность импульса, причем идет пояснение:
т.е. B - двусторонняя полоса в Герцах. Это очень важно, поскольку в статье про GMSK в выражении (1) параметр 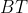 задается произведением односторонней полосы
задается произведением односторонней полосы 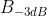 на длительность одного символа.
на длительность одного символа.
Второй параметр NT задает сколько символов надо учесть при фильтрации
Третий параметр OF задает количество отсчетов в одном символе.
Порядок фильтра определяется как 2*NT*OF+1, т.е. NT символов слева и NT символов справа каждый символ по OF отсчетов, плюс центральный отсчет.
Если мы откроем исходный код фильтра Гаусса в матлабе то увидим формулу по которой идет расчет:
Можно переписать это к более удобочитаемому виду:
 = \frac{\sqrt{\pi}}{\alpha} \cdot \exp \left( - \frac{\pi^2}{\alpha^2} \cdot t^2 \right ))
где
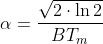
Параметр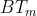 это BT в интерпретации матлаба
это BT в интерпретации матлаба
Если мы подставим то получим выражение для фильтра Гаусса в интерпретации матлаба вида:
то получим выражение для фильтра Гаусса в интерпретации матлаба вида:
 =BT_m \cdot \sqrt{ \frac{\pi}{2 \cdot \ln }} \cdot \exp \left( - \frac{\pi^2 \cdot BT_{m}^{2}}{2 \cdot \ln 2} \cdot t^2 \right ))
Заметим что в статье про GMSK выражение (1) при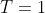 перепишется к виду:
перепишется к виду:
 =BT \cdot \sqrt{ \frac{ 2 \pi}{ \ln 2}} \cdot \exp \left( - \frac{2 \cdot \pi^2 \cdot BT^2}{ \ln 2} \cdot t^2 \right ))
Оба выражения верны, разница лишь в том, что при вычислении параметра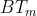 ( BT в интерпретации матлаба) использовалась двусторонняя полоса, а в статье односторонняя, соответственно можно сказать, что
( BT в интерпретации матлаба) использовалась двусторонняя полоса, а в статье односторонняя, соответственно можно сказать, что 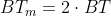 и если сделать такую подстановку, то получим что выражение для ИХ в интерпретации матлаба соответствует статье.
и если сделать такую подстановку, то получим что выражение для ИХ в интерпретации матлаба соответствует статье.
Зачем я это все так рассказываю? Затем, что я программировал свой фильтр гаусса и получал с матлабом различные результаты, пока не разобрался с этими односторонними и двусторонними полосами. Моя реализация фильтра Гаусса такая (функция на си):
она имеет несколько параметров:
double* g, - указатель на массив куда положить отсчеты ИХ
int Lg, - длина фильтра (размер массива g)
double BT, - BT (в интерпретации статьи)
int bc - задает сколько символов надо учесть при фильтрации (аналог матлабовского NT)
константа 28.477658649975010867721351422732 ничто иное как
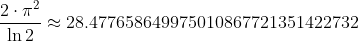
В таблице ниже представлены ИХ рассчитанные моей функцией и функцией матлаба
для фильтра Lg = 25 порядка (NT = bc = 3, OF = 4,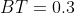 в интерпретации статьи и
в интерпретации статьи и 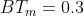 в интерпретации матлаба)
в интерпретации матлаба)
00_____________0.000000000_____________ 0.0004
01_____________0.000000001_____________ 0.0009
02_____________0.000000025_____________ 0.0021
03_____________0.000000523_____________ 0.0044
04_____________0.000007968_____________ 0.0087
05_____________0.000088083_____________ 0.0159
06_____________0.000706775_____________ 0.0267
07_____________0.004116537_____________ 0.0415
08_____________0.017403891_____________ 0.0595
09_____________0.053410195_____________ 0.0788
10_____________0.118977665_____________ 0.0962
11_____________0.192384558_____________ 0.1085
12_____________0.225807554_____________ 0.1129
13_____________0.192384558_____________ 0.1085
14_____________0.118977665_____________ 0.0962
15_____________0.053410195_____________ 0.0788
16_____________0.017403891_____________ 0.0595
17_____________0.004116537_____________ 0.0415
18_____________0.000706775_____________ 0.0267
19_____________0.000088083_____________ 0.0159
20_____________0.000007968_____________ 0.0087
21_____________0.000000523_____________ 0.0044
22_____________0.000000025_____________ 0.0021
23_____________0.000000001_____________ 0.0009
24_____________0.000000000_____________ 0.0004
Вполне очевидно, что значения различны ввиду различной интерпретации BT. Но если мы учтем что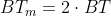 и построим таблицу при следующих параметрах: Lg = 25 порядка (NT = bc = 3, OF = 4,
и построим таблицу при следующих параметрах: Lg = 25 порядка (NT = bc = 3, OF = 4, 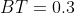 в интерпретации статьи и
в интерпретации статьи и  в интерпретации матлаба), то получим таблицу:
в интерпретации матлаба), то получим таблицу:
00_____________0.000000000_____________0.0000
01_____________0.000000001_____________0.0000
02_____________0.000000025_____________0.0000
03_____________0.000000523_____________0.0000
04_____________0.000007968_____________0.0000
05_____________0.000088083_____________0.0001
06_____________0.000706775_____________0.0007
07_____________0.004116537_____________0.0041
08_____________0.017403891_____________0.0174
09_____________0.053410195_____________0.0534
10_____________0.118977665_____________0.1190
11_____________0.192384558_____________0.1924
12_____________0.225807554_____________0.2258
13_____________0.192384558_____________0.1924
14_____________0.118977665_____________0.1190
15_____________0.053410195_____________0.0534
16_____________0.017403891_____________0.0174
17_____________0.004116537_____________0.0041
18_____________0.000706775_____________0.0007
19_____________0.000088083_____________0.0001
20_____________0.000007968_____________0.0000
21_____________0.000000523_____________0.0000
22_____________0.000000025_____________0.0000
23_____________0.000000001_____________0.0000
24_____________0.000000000_____________0.0000
Теперь результаты полностью совпадают.
Остается вопрос какая же интерпретация верная? графики в статье были построены при BT в интерпретации статьи. Вроде бы они согласуются с графиками приведенными в различных спецификациях на GSM.
Поскольку в разных источниках этот фильтр описан немного по-разному необходимо дать пояснения. Я буду опираться на матлаб и на собственную реализацию фильтра Гаусса, которые немного отличаются, я поясню в дальнейшем в чем именно. В матлабе фильтр Гаусса задается функцией gaussfir, в хелпе на нее написано следующее:
Код: Выделить всё
GAUSSFIR Gaussian FIR Pulse-Shaping Filter Design.
H=GAUSSFIR(BT) designs a low pass FIR gaussian pulse-shaping filter.
BT is the 3-dB bandwidth-symbol time product where B is the two-sided
bandwidth in Hertz and T is in seconds.
H=GAUSSFIR(BT,NT) NT is the number of symbol periods between the start
of the filter impulse response and its peak. If NT is not specified,
NT = 3 is used.
H=GAUSSFIR(BT,NT,OF) OF is the oversampling factor, that is, the number
of samples per symbol. If OF is not specified, OF = 2 is used.
The length of the impulse response of the filter is given by 2*OF*NT+1.
Also, the coefficients H are normalized so that the nominal passband
gain is always equal to one.
% EXAMPLE: Design a Gaussian filter to be used in a GSM GMSK scheme.
BT = .3; % 3-dB bandwidth-symbol time
OF = 8; % Oversampling factor (i.e., number of samples per symbol)
NT = 2; % 2 symbol periods to the filters peak.
h = gaussfir(BT,NT,OF);
hfvt = fvtool(h,'impulse');BT - ширина полосы фильтра по уровню -3 дБ умноженная на длительность импульса, причем идет пояснение:
Код: Выделить всё
B is the two-sided bandwidth in HertzВторой параметр NT задает сколько символов надо учесть при фильтрации
Третий параметр OF задает количество отсчетов в одном символе.
Порядок фильтра определяется как 2*NT*OF+1, т.е. NT символов слева и NT символов справа каждый символ по OF отсчетов, плюс центральный отсчет.
Если мы откроем исходный код фильтра Гаусса в матлабе то увидим формулу по которой идет расчет:
Код: Выделить всё
% Convert to t in which to compute the filter coefficients
t= convert2t(OF,NT);
% Equation 5.53 of [1]
alpha = sqrt(2*log(2))/(BT);
% Equation 5.54 of [1]
h = (sqrt(pi)/alpha)*exp(-(pi^2/alpha^2)*t.^2);
% Normalize coefficients
h = h./sum(h);
где
Параметр
Если мы подставим
Заметим что в статье про GMSK выражение (1) при
Оба выражения верны, разница лишь в том, что при вычислении параметра
Зачем я это все так рассказываю? Затем, что я программировал свой фильтр гаусса и получал с матлабом различные результаты, пока не разобрался с этими односторонними и двусторонними полосами. Моя реализация фильтра Гаусса такая (функция на си):
Код: Выделить всё
int filterGaussian(double* g, int Lg, double BT, int bc){
if((!g) || (Lg<=1) || (BT < 0.0))
return 0;
double dt = (double)bc * 2.0/(double)(Lg-1);
double t;
double beta = 28.477658649975010867721351422732 * BT * BT;
t = -(double)bc-dt;
double sg = 0.0;
for(int i = 0; i<Lg; i++){
t += dt;
g[i] = exp(-beta*t*t);
sg+=g[i];
}
for(int i = 0; i<Lg; i++){
g[i] /= sg;
}
return 1;
}
double* g, - указатель на массив куда положить отсчеты ИХ
int Lg, - длина фильтра (размер массива g)
double BT, - BT (в интерпретации статьи)
int bc - задает сколько символов надо учесть при фильтрации (аналог матлабовского NT)
константа 28.477658649975010867721351422732 ничто иное как
В таблице ниже представлены ИХ рассчитанные моей функцией и функцией матлаба
для фильтра Lg = 25 порядка (NT = bc = 3, OF = 4,
00_____________0.000000000_____________ 0.0004
01_____________0.000000001_____________ 0.0009
02_____________0.000000025_____________ 0.0021
03_____________0.000000523_____________ 0.0044
04_____________0.000007968_____________ 0.0087
05_____________0.000088083_____________ 0.0159
06_____________0.000706775_____________ 0.0267
07_____________0.004116537_____________ 0.0415
08_____________0.017403891_____________ 0.0595
09_____________0.053410195_____________ 0.0788
10_____________0.118977665_____________ 0.0962
11_____________0.192384558_____________ 0.1085
12_____________0.225807554_____________ 0.1129
13_____________0.192384558_____________ 0.1085
14_____________0.118977665_____________ 0.0962
15_____________0.053410195_____________ 0.0788
16_____________0.017403891_____________ 0.0595
17_____________0.004116537_____________ 0.0415
18_____________0.000706775_____________ 0.0267
19_____________0.000088083_____________ 0.0159
20_____________0.000007968_____________ 0.0087
21_____________0.000000523_____________ 0.0044
22_____________0.000000025_____________ 0.0021
23_____________0.000000001_____________ 0.0009
24_____________0.000000000_____________ 0.0004
Вполне очевидно, что значения различны ввиду различной интерпретации BT. Но если мы учтем что
00_____________0.000000000_____________0.0000
01_____________0.000000001_____________0.0000
02_____________0.000000025_____________0.0000
03_____________0.000000523_____________0.0000
04_____________0.000007968_____________0.0000
05_____________0.000088083_____________0.0001
06_____________0.000706775_____________0.0007
07_____________0.004116537_____________0.0041
08_____________0.017403891_____________0.0174
09_____________0.053410195_____________0.0534
10_____________0.118977665_____________0.1190
11_____________0.192384558_____________0.1924
12_____________0.225807554_____________0.2258
13_____________0.192384558_____________0.1924
14_____________0.118977665_____________0.1190
15_____________0.053410195_____________0.0534
16_____________0.017403891_____________0.0174
17_____________0.004116537_____________0.0041
18_____________0.000706775_____________0.0007
19_____________0.000088083_____________0.0001
20_____________0.000007968_____________0.0000
21_____________0.000000523_____________0.0000
22_____________0.000000025_____________0.0000
23_____________0.000000001_____________0.0000
24_____________0.000000000_____________0.0000
Теперь результаты полностью совпадают.
Остается вопрос какая же интерпретация верная? графики в статье были построены при BT в интерпретации статьи. Вроде бы они согласуются с графиками приведенными в различных спецификациях на GSM.
-
Виктор Васильевич
- Сообщения: 11
- Зарегистрирован: 23 окт 2012, 11:16
Re: ИХ фильтра Гаусса
не так давно реализовывал частотную телеграфию, и для этого использовал фильтр Гаусса для сглаживания фронтов. когда реализовывал, при вычислении коэффициентов фильтра Гаусса (h = gaussfir(BT,NT,OF)), параметр BT взял c головы... сейчас возник вопрос, каким образом выбирается ширина полосы фильтра Гаусса по уровню 3 дБ(B), чтобы сглаживание фронтов было оптимальным? чем она определяется (B)? от нее зависит степень сглаживания фронтов...
BT - ширина полосы фильтра по уровню -3 дБ (B) умноженная на длительность импульса(T). т.е. BT = B*T. спасибо.
BT - ширина полосы фильтра по уровню -3 дБ (B) умноженная на длительность импульса(T). т.е. BT = B*T. спасибо.
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: ИХ фильтра Гаусса
Важен параметр BT чем меньше тем сигнал будет более сглаженный (спектр будет более узкий) но сильнее будет межсимвольная интерференция. Реально минимально используемый BT = 0.3 если меньше то демодулировать без ошибок невозможно.
-
Виктор Васильевич
- Сообщения: 11
- Зарегистрирован: 23 окт 2012, 11:16
Re: ИХ фильтра Гаусса
спасибо, я это все понимаю. мне просто важно знать, каким образом выбрать оптимальное значение коэффициента BT. при минимально допустимом значении 0.3, сглаживание фронтов настолько сильное, что при не повторяющем(не групповом, а единичном) символе, сигнал не успевает дорасти до максимального значения, как уже начинает спадать.Важен параметр BT чем меньше тем сигнал будет более сглаженный (спектр будет более узкий) но сильнее будет межсимвольная интерференция.
-
humbert_humbert
- Сообщения: 18
- Зарегистрирован: 25 сен 2019, 11:30
Re: ИХ фильтра Гаусса
Здравствуйте. Я тоже разбираюсь с GMSK, и чтобы не плодить темы, задам вопрос здесьБахурин Сергей писал(а): ↑05 янв 2011, 16:17Ну что-же в данном длинном посте я постараюсь изложить свои соображения по поводу ких фильтра Гаусса для GMSK.
На сколько мне известно, GMSK - это тоже самое, что и MSK, только фазовая характеристика не прямоугольная, а сглажена фильтром гаусса.
ниже привожу мой код модулятора MSK.
Код: Выделить всё
function [signal] = MSK_Modulator(symbols,m,Fs,Fd,h)
map = (0:2^m-1)*2-(2^m -1);
PAM = map(symbols+1)/2;
PAM = upsample(PAM,Fs/Fd);
PAM = filter(ones(1,Fs/Fd),1,PAM);%Фазовая характеристика
Freq = 2*pi*h*PAM/(Fs/Fd);
Phase = cumsum(Freq);%Частотная характеристика
signal = exp(1i*Phase);
end
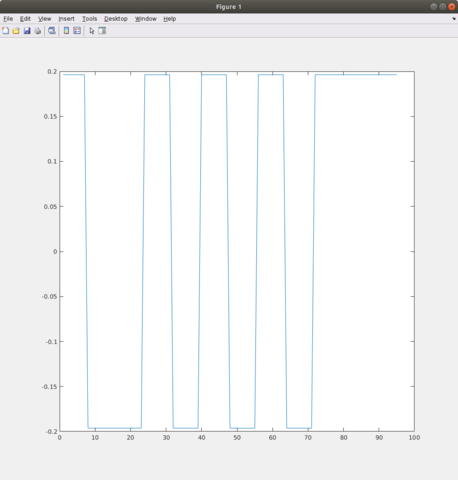
Видно, что вроде бы все нормально. К тому же результат работы моего модулятора совпадает с матлабовским comm.MSKModulator.
Далее, чтобы получить gmsk, я добавляю гауссовский фильтр:
Код: Выделить всё
function [signal] = GMSK_Modulator(symbols,m,Fs,Fd,h,BT)
windowCoeff = gaussdesign(BT,1,Fs/Fd);%Фильтр гаусса
map = (0:2^m-1)*2-(2^m -1);
PAM = map(symbols+1)/2;
PAM = upsample(PAM,Fs/Fd);
PAM = filter(ones(1,Fs/Fd),1,PAM);
PAM = filter(windowCoeff,1,PAM);
Freq = 2*pi*h*PAM/(Fs/Fd);
Phase = cumsum(Freq);
signal = exp(1i*Phase);
end
График разности фаз:
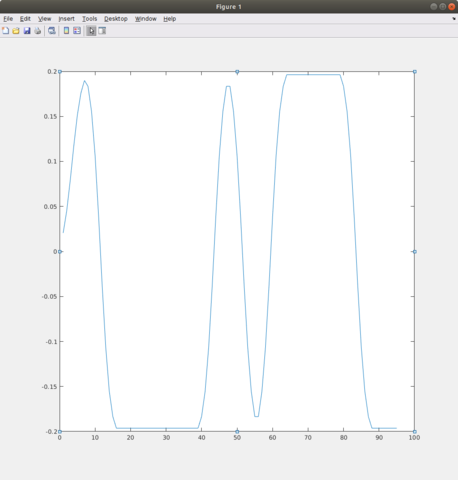
Вроде бы результат правильный, но я не уверен в этом, так как матлабовский comm.GMSKModulator('BitInput',true,'BandwidthTimeProduct',0.5,'PulseLength',1,'SamplesPerSymbol',Fs/Fd) выдает такой такой график разности фаз:
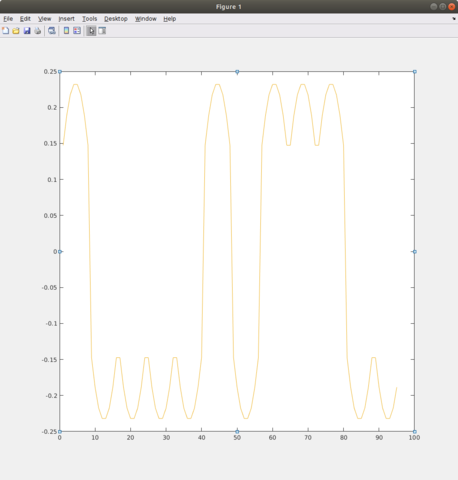
Вопрос: правильно ли я все сделал, и если ошибся, то в чем?
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: ИХ фильтра Гаусса
Если честно ваш график выглядит более правдоподобным по сравнению с матлабовским тулбоксом. К сожалению тулбокса нет, не могу проверить
-
humbert_humbert
- Сообщения: 18
- Зарегистрирован: 25 сен 2019, 11:30
Re: ИХ фильтра Гаусса
Кажется, я понял в чем дело. В параметрах матлабовского демодулятора я выбрал параметр "Pulse Length' равным 1. Поэтому и график такой получается.Бахурин Сергей писал(а): ↑24 дек 2019, 15:01Если честно ваш график выглядит более правдоподобным по сравнению с матлабовским тулбоксом. К сожалению тулбокса нет, не могу проверить
Если сделать его равным 4, а в моем модуляторе установить параметр filter span = 4 в функции для генерации коэффициентов фильтра, то графики будут одинаковыми.
Re: ИХ фильтра Гаусса
Добрый вечер.
Такой вопрос, по поводу интерполяции, и фильтрации с помощью фильтра Гаусса.
По Лайонсу, интерполируют дополняя 0 исходный сигнал, а затем фильтруют, что бы подавить образы.
MATLAB GMSK делает это таким же методом, но результат отличается от того что приведено в статье, и я экспериментировал, если интерполировать 0, и применять ФГ, получается тоже самое что в матлабе, но абсолютно не тоже самое что в статье.
Какие соображения по этому поводу?
Такой вопрос, по поводу интерполяции, и фильтрации с помощью фильтра Гаусса.
По Лайонсу, интерполируют дополняя 0 исходный сигнал, а затем фильтруют, что бы подавить образы.
MATLAB GMSK делает это таким же методом, но результат отличается от того что приведено в статье, и я экспериментировал, если интерполировать 0, и применять ФГ, получается тоже самое что в матлабе, но абсолютно не тоже самое что в статье.
Какие соображения по этому поводу?
- Бахурин Сергей
- Администратор
- Сообщения: 1116
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: ИХ фильтра Гаусса
В чем разница? По идее при одинаковых параметрах фильтра гаусса разницы быть не должно. Чуть выше приведено разъяснение разной интерпретации параметров фильтра гаусса.
